Фото: arXiv.org
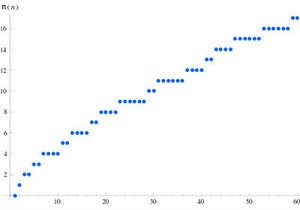
Значення пі-функції для перших 50 натуральних значень
Іспанські вчені Хосе Латорре та Герман Сьєрра розробили ефективний квантовий алгоритм обчислення пі-функції.
Пі-функція π (k) дорівнює кількості простих
(тобто таких, що діляться лише на себе і на одиницю) чисел, не більших за k. Ця
функція є найважливішим елементом сучасної теорії чисел.
У рамках роботи вчені розглядали систему з n
кубітів - квантових бітів, здатних перебувати у суперпозиції двох станів.
За допомогою послідовного застосування вже
відомих квантових алгоритмів (наприклад, алгоритм Гровера для пошуку рішення
рівнянь для булевих функцій) вдалося побудувати стан, який відповідає деякій
суперпозиції усіх простих чисел, які не більші за 2n. Цей стан вчені назвали
простим станом (prime state).
Вчені зазначають, що отриманий стан можна
застосувати для підрахунку кількості простих чисел-близнюків - простих чисел,
різниця між якими дорівнює двом. Учені поки що не змогли визначити, скінченна чи
нескінченна множина таких чисел.
Дослідники стверджують, що їхній алгоритм
виконує обчислення набагато ефективніше від класичних алгоритмів.
Нагадаємо, що минулого року Нобелівську премію
з фізики було присуджено французькому вченому Сержу Арошу та американському
досліднику Девіду Уайнленду за відкриття експериментальних методів вимірювання
та маніпулювання індивідуальними квантовими системами.